이번 장에서는 DFS & BFS 알고리즘을 사용하여 Graph를 탐색해본다.
모든 코드는 깃허브 (링크)의 테스트 코드로 정리해두었다.
그래프와 종류
그래프(Graph)는 Graph (V, E)라고도 표기하며 각각의 노드를 뜻하는 Vertex와 노드를 연결하는 간선을 의미하는 Edge의 집합이다.
무방향 그래프
Vertex를 연결하는 Edge에 방향이 없이 연결되어 있는 그래프.
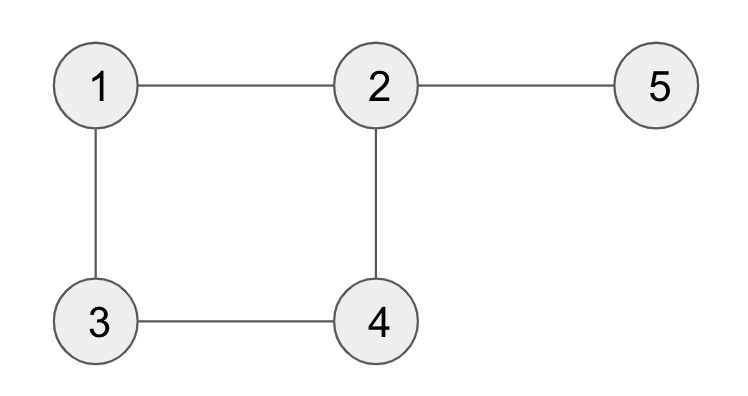
이러한 그래프의 연결관계를 이차원 배열로 나타내면 아래와 같다.
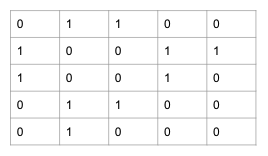
1과 2는 서로 연결되어 있으므로 1,2와 2,1은 1이다. 2와 4도 서로 연결되어 있으므로 2,4와 4,2는 1이다.
5와 4는 서로 연결되어 있지 않으므로 5,4와 4,5는 0이다.
방향 그래프
Vertex를 연결하는 Edge에 방향이 존재하는 상태로 연결되어 있는 그래프.
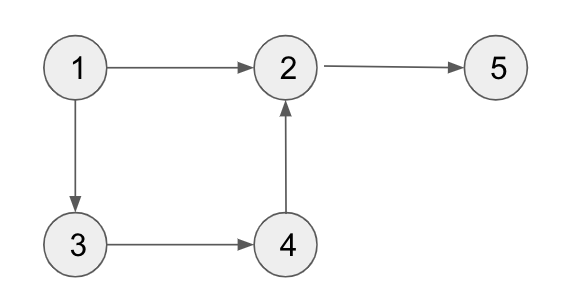
이러한 그래프의 연결관계를 이차원 배열로 나타내면 아래와 같다.
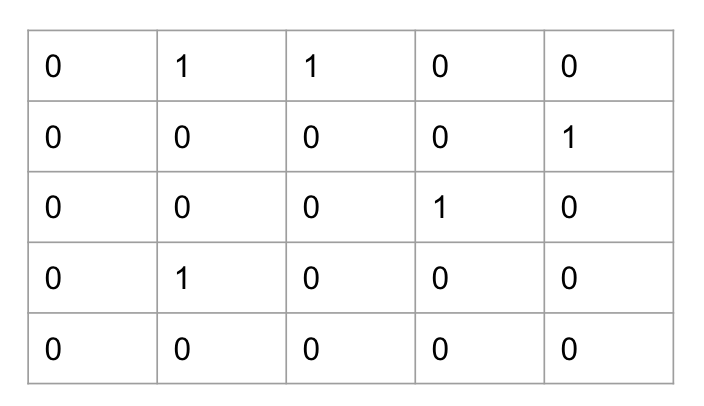
1과 2는 서로 연결되어 있지만 1 -> 2 방향으로 연결되어 있기 때문에 1,2 = 1이지만 2,1은 0이다.
가중치 그래프
Vertex를 연결하는 Edge에 방향과 가중치가 존재하는 상태로 연결되어 있는 그래프.
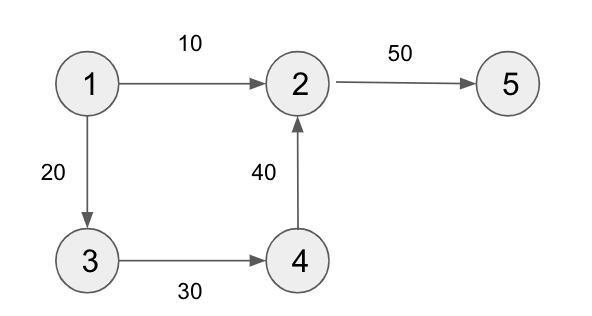
이러한 그래프의 연결관계를 이차원 배열로 나타내면 아래와 같다.
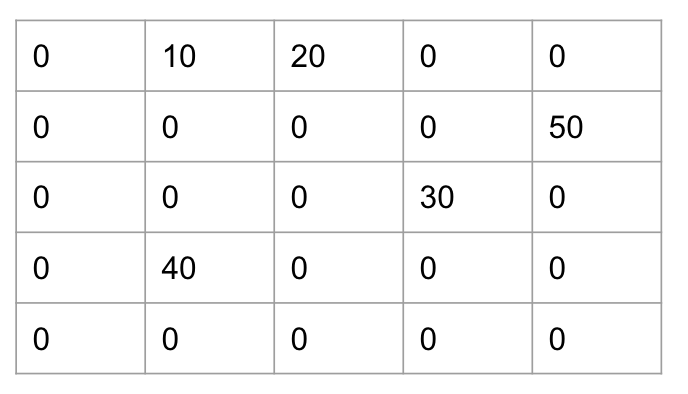
1과 2는 서로 연결되어 있지만 1 -> 2 방향으로 연결되어 있기 때문에 2,1은 0이다.
또한 1 -> 2의 가중치는 10이기 때문에 1,2는 1이 아닌 10이다.
경로 탐색(인접행렬)
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요.
아래 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는
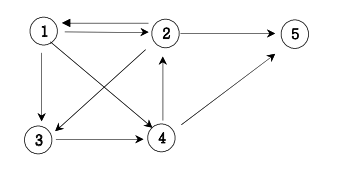
1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 5 가지입니다.
- 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다. - 출력설명
총 가지수를 출력한다. - 입력예제 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5 - 출력예제 1
6
public class PathSearchByArray {
private static final int VERTEXES = 5;
private static final int[] CHECK_ARRAY = new int[VERTEXES + 1];
private static final int[][] CONNECTIONS = {
{1, 2}, {1, 3}, {1, 4},
{2, 1}, {2, 3}, {2, 5},
{3, 4}, {4, 2}, {4, 5}
};
private int[][] graph;
private int answer = 0;
public void solution1(int vertex) {
if (vertex == VERTEXES) {
answer++;
}
for (int i = 1; i <= VERTEXES; i++) {
if (graph[vertex][i] == 1 && CHECK_ARRAY[i] == 0) {
CHECK_ARRAY[i] = 1;
solution1(i);
CHECK_ARRAY[i] = 0;
}
}
}
@Test
@DisplayName("경로 탐색(인접행렬)")
public void main() {
int expectedAnswer = 6;
graph = new int[VERTEXES + 1][VERTEXES + 1];
Arrays.stream(CONNECTIONS).forEach(connection ->
graph[connection[0]][connection[1]] = 1
);
CHECK_ARRAY[1] = 1;
solution1(1);
assertEquals(expectedAnswer, answer);
}
}경로 탐색(인접리스트)
문제는 경로 탐색(인접행렬)과 동일
public class PathSearchByList {
private static final int VERTEXES = 5;
private static final int[] CHECK_ARRAY = new int[VERTEXES + 1];
private static final int[][] CONNECTIONS = {
{1, 2}, {1, 3}, {1, 4},
{2, 1}, {2, 3}, {2, 5},
{3, 4}, {4, 2}, {4, 5}
};
private final List<ArrayList<Integer>> graph = new ArrayList<>();
private int answer = 0;
public void solution1(int vertex) {
if (vertex == VERTEXES) {
answer++;
} else {
for (int nextVertex : graph.get(vertex)) {
if (CHECK_ARRAY[nextVertex] == 0) {
CHECK_ARRAY[nextVertex] = 1;
solution1(nextVertex);
CHECK_ARRAY[nextVertex] = 0;
}
}
}
}
@Test
@DisplayName("경로 탐색(인접리스트)")
public void main() {
int expectedAnswer = 6;
for (int i = 1; i <= VERTEXES; i++) {
graph.add(new ArrayList<>());
}
Arrays.stream(CONNECTIONS).forEach(connection ->
graph.get(connection[0]).add(connection[1])
);
CHECK_ARRAY[1] = 1;
solution1(1);
assertEquals(expectedAnswer, answer);
}
}그래프 최단 거리(BFS)
다음 그래프에서 1번 정점에서 각 정점으로 가는 최소 이동 간선수를 출력하세요.
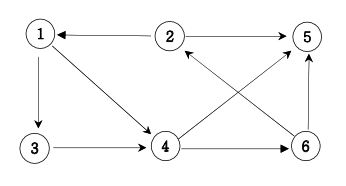
- 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다. - 출력설명
1번 정점에서 각 정점으로 가는 최소 간선수를 2번 정점부터 차례대로 출력하세요. - 입력예제 1
6 9
1 3
1 4
2 1
2 5
3 4
4 5
4 6
6 2
6 5 - 출력예제 1
2 3
3 1
4 1
5 2
6 2
public class ShortestPath {
private static final int VERTEXES = 6;
private static final int[] CHECK_ARRAY = new int[VERTEXES + 1];
private static final int[] EXPECTED_DISTANCES = {0, 0, 3, 1, 1, 2, 2};
private static final int[] DISTANCES = new int[VERTEXES + 1];
private static final int[][] CONNECTIONS = {
{1, 3}, {1, 4},
{2, 1}, {2, 5},
{3, 4},
{4, 5}, {4, 6},
{6, 2}, {6, 2}
};
private final List<ArrayList<Integer>> graph = new ArrayList<>();
public void solution1(int vertex) {
Queue<Integer> queueOfVertex = new LinkedList<>();
CHECK_ARRAY[vertex] = 1;
DISTANCES[vertex] = 0;
queueOfVertex.offer(vertex);
while(!queueOfVertex.isEmpty()) {
int currentVertex = queueOfVertex.poll();
for (int nextVertex : graph.get(currentVertex)) {
if (CHECK_ARRAY[nextVertex] == 0) {
CHECK_ARRAY[nextVertex] = 1;
queueOfVertex.offer(nextVertex);
DISTANCES[nextVertex] = DISTANCES[currentVertex] + 1;
}
}
}
}
@Test
@DisplayName("그래프 최단거리(BFS)")
public void main() {
for (int i = 0; i <= VERTEXES; i++) {
graph.add(new ArrayList<>());
}
for (int[] connection : CONNECTIONS) {
graph.get(connection[0]).add(connection[1]);
}
solution1(1);
assertArrayEquals(EXPECTED_DISTANCES, DISTANCES);
}
}'Algorithm' 카테고리의 다른 글
| [Algorithm] BFS 활용 (0) | 2022.03.01 |
|---|---|
| [Algorithm] DFS 활용 (0) | 2022.03.01 |
| [Algorithm] DFS 원리 (0) | 2022.02.28 |
| [Algorithm] DFS & BFS 기본문제 (0) | 2022.02.28 |
| [Algorithm] Recursive (0) | 2022.02.27 |



