🧪 화학 평형과 평형 상수 ($K$)
핵심 내용: 동적 평형의 개념, 평형 상수 식 세우기($K_c, K_p$), $Q$값(반응지수)과 $K$값 비교를 통한 반응 진행 방향 예측.
물을 컵에 담아두면 다 증발해 버린다. 이건 한쪽으로만 가는 반응이다.
하지만 밀폐된 용기 안에서는 물이 줄어들다가 어느 순간 멈춘 것처럼 보인다.
화학 반응도 마찬가지다. 반응물이 전부 생성물로 바뀌고 끝나는 게 아니라, 어느 정도 가다가 "적당한 선에서 타협"을 본다. 이것이 바로 화학 평형이다.
1. 동적 평형 상태 (Dynamic Equilibrium)
가장 중요한 개념이다. 겉보기엔 멈춘 것 같지만, 속에서는 미친듯이 바쁘다.
- 가역 반응: 정반응(오른쪽)과 역반응(왼쪽)이 모두 일어날 수 있는 반응. ($\rightleftharpoons$ 화살표 사용)
- 동적 평형의 정의:
- 속도: 정반응 속도와 역반응 속도가 같아진 상태 ($v_{\text{정}} = v_{\text{역}}$).
- 농도: 반응물과 생성물의 농도가 일정하게 유지되는 상태. (농도가 같다는 뜻이 아님!)

💡 그래프 해석 팁:
- 속도 그래프: 두 선이 만나서 하나가 되면 평형 도달.
- 농도 그래프: 두 선이 만나지 않아도 됨. 기울기가 0(평평해짐)이 되면 평형 도달.
2. 평형 상수 ($K$, Equilibrium Constant)
평형 상태에서 물질들이 '어떤 비율'로 섞여 있는지를 나타내는 값이다. 화학2 계산의 알파이자 오메가다.
(1) 평형 상수 식
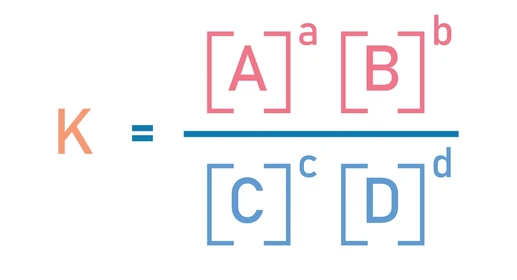
반응식: $aA + bB \rightleftharpoons cC + dD$
$$K = \frac{[C]^c [D]^d}{[A]^a [B]^b}$$
(분모: 반응물 농도 곱 / 분자: 생성물 농도 곱)
(2) 반드시 지켜야 할 3가지 규칙
- 고체($s$)와 액체($l$)는 생략한다: 농도(밀도)가 변하지 않기 때문. 기체($g$)와 수용액($aq$)만 식에 넣는다.
- 계수가 곧 지수다: 반응식의 계수($a,b,c,d$)가 농도의 지수로 올라간다.
- 온도($T$)가 변해야만 $K$가 변한다: 농도나 압력을 바꿔도 $K$ 값 자체는 절대 변하지 않는다. (매우 중요!)
3. 반응의 진행 방향 예측 ($Q$ vs $K$)
지금 이 순간, 반응이 평형인지 아니면 평형을 향해 가고 있는지 어떻게 알까?
현재 농도를 평형 상수 식에 때려 넣은 값, 반응 지수($Q$)와 평형 상수($K$)를 비교하면 된다.
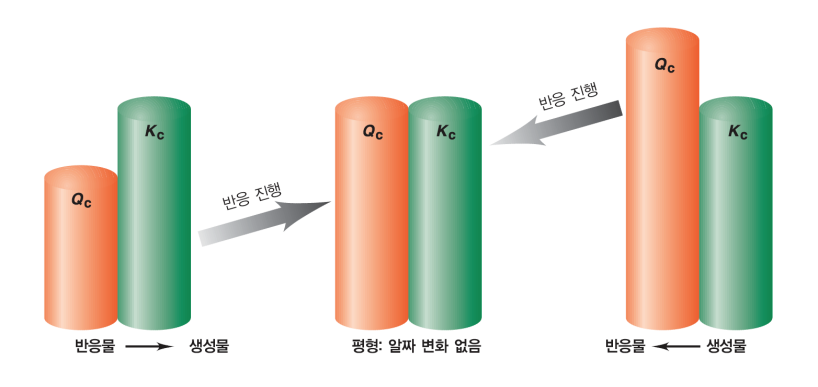
- $Q < K$ (분모가 큼): 생성물이 부족하다. $\rightarrow$ 정반응 진행 (오른쪽으로 이동)
- $Q = K$: 현재 평형 상태다.
- $Q > K$ (분자가 큼): 생성물이 너무 많다. $\rightarrow$ 역반응 진행 (왼쪽으로 이동)
4. 르 샤틀리에 원리 (평형 이동의 법칙)
자연은 변화를 싫어한다. 이것이 르 샤틀리에 원리의 핵심이다.
평형 상태인 계에 어떤 변화(스트레스)를 주면, 그 변화를 상쇄시키는 방향으로 평형이 이동한다.
① 농도 변화
- 반응물 첨가: 반응물을 없애기 위해 $\rightarrow$ 정반응 진행
- 생성물 제거: 생성물을 다시 만들기 위해 $\rightarrow$ 정반응 진행
② 압력(부피) 변화 (기체 반응에서만)
- 압력 증가 (부피 감소): 좁아졌으니 붐비는 게 싫다. $\rightarrow$ 기체 분자 수가 감소하는 방향으로 이동.
- (예: $N_2 + 3H_2 \rightleftharpoons 2NH_3$ 에서 압력을 높이면, 계수 합이 4에서 2로 줄어드는 정반응 쪽으로 이동)
③ 온도 변화 (유일하게 $K$값이 변함)
- 온도 높임: 뜨거운 게 싫어서 열을 흡수하려 한다. $\rightarrow$ 흡열 반응 쪽으로 이동.
- 온도 낮춤: 차가운 게 싫어서 열을 방출하려 한다. $\rightarrow$ 발열 반응 쪽으로 이동.
⚠️ 주의: 촉매의 역할
촉매는 반응 속도만 빠르게 해줄 뿐, 평형 상수를 바꾸거나 평형 위치를 이동시키지 못한다. (단지 평형에 더 빨리 도달하게 해줄 뿐이다.)
5. 핵심 요약
- 동적 평형: 정반응 속도 = 역반응 속도. 멈춘 게 아니다.
- 평형 상수($K$): $\frac{\text{생성물}}{\text{반응물}}$. 고체/액체 제외. 오직 온도에 의해서만 값이 변한다.
- 방향 예측: $Q < K$이면 정반응, $Q > K$이면 역반응.
- 르 샤틀리에 원리:
- 압력 $\uparrow$ $\rightarrow$ 기체 몰수 적은 쪽
- 온도 $\uparrow$ $\rightarrow$ 흡열 반응 쪽
- 촉매: 평형 이동 $X$, $K$값 변화 $X$. (시간 단축 $O$)
'Chemistry > 심화' 카테고리의 다른 글
| 8. 산 · 염기 평형과 pH (0) | 2025.12.11 |
|---|---|
| 7. 르 샤틀리에 원리 (평형 이동의 법칙) (0) | 2025.12.11 |
| 5. 반응 엔탈피와 헤스의 법칙 (0) | 2025.12.11 |
| 4. 용액의 농도와 총괄성 (0) | 2025.12.11 |
| 3. 분자 간의 힘과 물질의 상태 (0) | 2025.12.11 |



